t-SNE

Open Table of contents

1. Khái niệm liên quan
- 1.1. Dimensional Reduction
- 1.2. Stochastic Neighbor Embedding
2. Khái niệm chính
- 2.1. t-SNE
3. Implement Code
- 3.1. Xử lý data
- 3.2. Main class

1. Khái niệm liên quan

1.1. Dimensional Reduction

Là hình thức giảm chiều của dữ liệu xuống để có thể biểu diễn trong không gian số chiều nhỏ hơn với mục đích dễ xử lý hơn. Chính vì thế, các kĩ thuật phải đảm bảo giữ được thông tin quan trọng

Các kĩ thuật giảm chiều được xếp vào 2 loại:

Giảm chiều tuyến tính: dành cho dữ liệu có thể biểu diễn bằng các mối quan hệ tuyến tính. Một vài kĩ thuật như: PCA,
Giảm chiều phi tuyến tính: dành cho dữ liệu có cấu trúc phức tạp, đảm bảo các mối quan hệ phi tuyến tính của dữ liệu gốc. Một vài kĩ thuật như: t-SNE, Isomap

1.2. Stochastic Neighbor Embedding

Các phương pháp khác cố gắng tạo mối liên kết giữa các điểm trong không gian nhiều chiều thành “fixed grid of point” ở không gian có số chiều thấp. Tuy nhiên việc bắt mỗi object ở không gian nhiều chiều thành một điểm ở không gian thấp hơn gây khó khăn. Bởi thực tế một object mơ hồ thuộc về nhiều điểm khác loại hơn.

Do đó ta có phương pháp stochastic neighbor embedding

2. Khái niệm chính

2.1. t-SNE

Xây dựng hàm mapping mà khoảng cách giữa các điểm phản ảnh sự tương đồng ở trong tệp dữ liệu. Cũng cần phải giảm thiểu số lượng hàm objective mà dùng để tính toán sự không thống nhất giữa sự tương đồng trong tệp dữ liệu và sự tương đồng trong hàm mapping

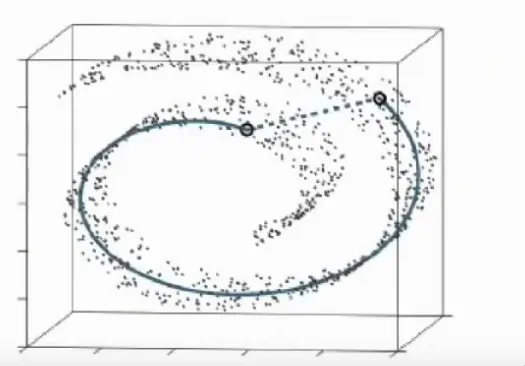
Khác với các phương pháp khác như PCA, images

Xét trường hợp cặp điểm như trên mặc dù Euclidean Distance nhỏ nhưng lại không có điểm tương đồng. Phương pháp PCA mục đích duy trì general structure của dữ liệu qua việc giữ lại những cặp có khoảng cách lớn

Vậy làm sao để duy trì những cặp có khoảng cách nhỏ?

2.1.1. High-D

Phương pháp t-SNE hướng tới việc giữ lại những cặp gần nhau trong local structure.

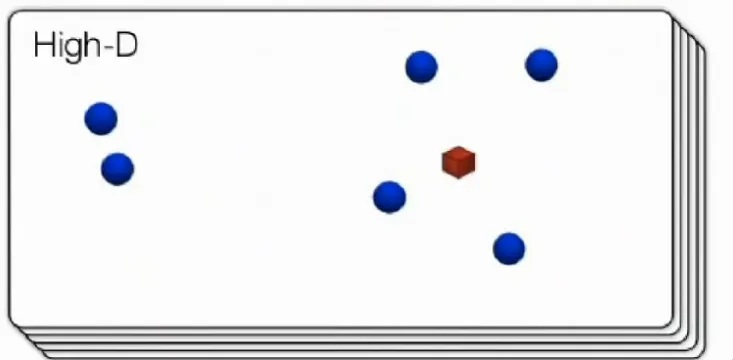
Cụ thể hơn, ở không gian nhiều chiều: images

Xét điểm đỏ là $x_i$ và điểm xanh xung quanh là $x_j$

p_{ij} = \frac{\exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2\sigma^2}\right)}{\sum_k \sum_{l \neq k} \exp\left(-\frac{\|\mathbf{x}_k - \mathbf{x}_l\|^2}{2\sigma^2}\right)}

Khi đó ta sẽ thực hiện Gaussian, cho các điểm ở trong local structure. Từ khoảng cách của các điểm ta biển đổi thành chỉ số tương đồng, điểm càng gần thì chỉ số càng cao.

\exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2\sigma^2}\right)

Sau đó, thực hiện normalize

\sum_k \sum_{l \neq k} \exp\left(-\frac{\|\mathbf{x}_k - \mathbf{x}_l\|^2}{2\sigma^2}\right)

Cuối cùng ta được một probability distribution trên những cặp điểm, mà xác suất chọn một cặp bất kì tỉ lệ thuận với sự tương đồng. Do đó, nếu hai điểm gần nhau ở không gian nhiều chiều thì $p_{ij}$ càng lớn. Ngược lại nếu hai điểm càng xa thì $p_{ij}$ vô cùng nhỏ.

Symmetrize the conditionals:

p_{ij} = \frac{p_{j|i} + p_{i|j}}{2N}

2.1.2. Low-D

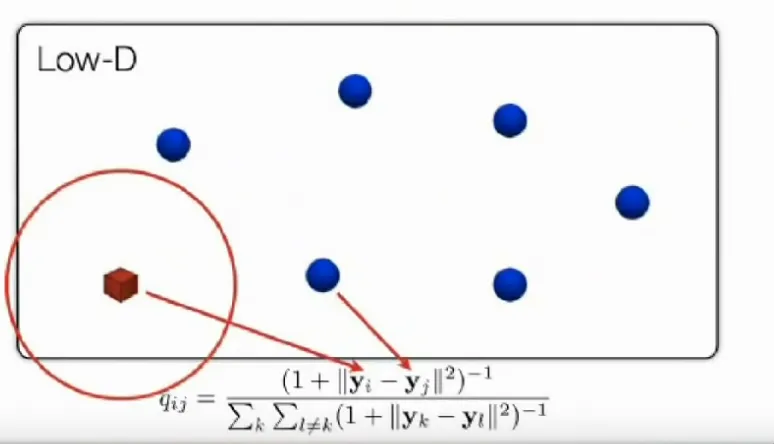
images

q_{ij} = \frac{(1 + \|\mathbf{y}_i - \mathbf{y}_j\|^2)^{-1}}{\sum_k \sum_{l \neq k} (1 + \|\mathbf{y}_k - \mathbf{y}_l\|^2)^{-1}}

Thực hiện thao tác tương tự như ở không gian nhiều chiều.

Khi đó, chúng ta muốn $q_{ij}$ phản ánh $p_{ij}$ nhiều nhất có thể để structure của Low-D map giống với lại structure của dữ liệu ở High-D

Để tính toán được sự khác biệt này, ta dùng Kullback–Leibler divergence

KL(P \| Q) = \sum_i \sum_{j \neq i} p_{ij} \log \frac{p_{ij}}{q_{ij}}

2.1.3. Crowding Problem

Ở không gian nhiều chiều sẽ có rất nhiều khoảng trống. Do đó một điểm có thể có rất nhiều điểm lân cận.

Giả sử ở không gian 2D, một điểm có một số điểm lân cận gần với điểm đó. Nhưng các điểm lân cận này lại cách xa nhau. Khi các điểm từ 2D được duy trì xuống 1D, các điểm lân cận vốn cách xa nhau lại được xếp gần nhau. Chính vì thế ta cần một distribution vẫn giữ được structure của điểm gần nhau và structure của các điểm xa nhau.

Những distribution có đuôi nối dài tới vô cùng sẽ giúp ích: Gaussian Distribution và Student-t Distribution

Về tại sao lại không dùng gaussian ở Low-D. Ta sẽ dùng một khái niệm mới là Student-t Distribution:

(1 + \|\mathbf{y}_i - \mathbf{y}_j\|^2)^{-1}

Student-t Distribution giống với Gaussian Distribution nhưng with heavier tails, nghĩa là nó có thể giải quyết những extreme values và trường hợp tập dữ liệu ít.

Giả sử nếu như trong Gaussian Distribution, hai điểm cách xa 10 20 đơn vị, ta được density là 0.01 . Thì để được density như vậy ở trong Student-t Distribution, hai điểm phải cách xa ví dụ 20 30 đơn vị. Như vậy, ta đạt được mục đích là duy trì được local structure và làm mờ đi những điểm rất xa nhau.

3. Implement Code

3.1. Xử lý data

Dạng của dataset: TSNE khá là expensive và phát huy sức mạnh khi xủ lý các dataset có nhiều mối quan hệ phi tuyến tính, với những cụm phức tạp.

Lựa chọn dataset với tầm 1000-2000 samples, 10-20 features và 2-4 clusters.

Chọn MNIST Dataset

Table of contents