Table of contents
Open Table of contents
1. Các khái niệm liên quan
1.1. Smooth Function
Có tính chất infinitely differentiable .
1.2. Complex Space
Kí hiệu: C \mathbb{C} C
2. Các khái niệm chính
2.1. Taylor Series
Mục đích: để có một function khác giống function đang tìm hiểu.
ELI5: Biến một đường cong xấu xí thành một đường cong dịu dàng
Taylor Polynomial: bậc n của hàm f : R → R f:\mathbb{R} \to \mathbb{R} f : R → R x 0 x_{0} x 0
T n ( x ) : = ∑ k = 0 n f ( k ) ( x 0 ) k ! ( x − x 0 ) k T_n(x):=\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k T n ( x ) := k = 0 ∑ n k ! f ( k ) ( x 0 ) ( x − x 0 ) k Taylor Series: f ∈ C ∞ f \in \mathbb{C}^{\infty} f ∈ C ∞
T ∞ ( x ) : = ∑ k = 0 ∞ f ( k ) ( x 0 ) k ! ( x − x 0 ) k T_\infty(x):=\sum_{k=0}^\infty\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k T ∞ ( x ) := k = 0 ∑ ∞ k ! f ( k ) ( x 0 ) ( x − x 0 ) k is called analytic if f ( x ) = T ∞ ( x ) f(x)=T_{\infty}(x) f ( x ) = T ∞ ( x )
2.2. Partial Differentiation và Gradient
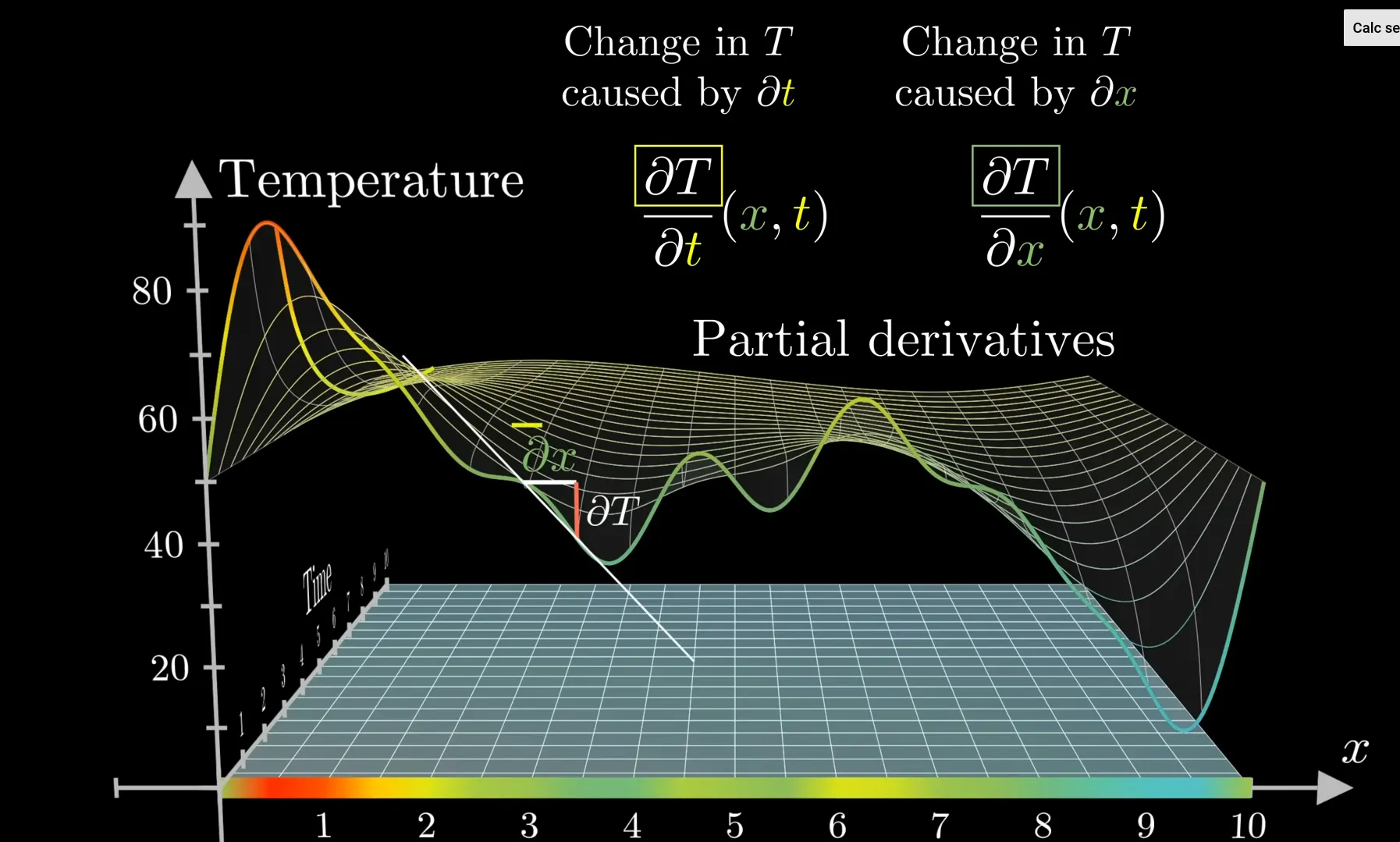
Khác với Differentiation thông thường , partial tức là chỉ nói về một phần của derivative.
Lấy ví dụ về sự thay đổi nhiệt độ trong không gian: ta sẽ có derivative của nhiệt độ T theo vị trí x trong không gian, và derivative của nhiệt độ T theo thời gian t . Như vậy equation chỉ có thể nói về một phần của sự thay đổi .
Gradient chứa thông tin của các partial derivatives dưới dạng vector .
∇ f = [ ∂ f ∂ x ∂ f ∂ y ⋮ ] \nabla f =
\begin{bmatrix}
\dfrac{\partial f}{\partial x} \\\\
\dfrac{\partial f}{\partial y} \\\\
\vdots
\end{bmatrix} ∇ f = ∂ x ∂ f ∂ y ∂ f ⋮ 2.2.1. Các quy tắc
Quy tắc nhân :
∂ ∂ x ( f ( x ) g ( x ) ) = ∂ f ∂ x g ( x ) + f ( x ) ∂ g ∂ x \frac{\partial}{\partial x}\left(f(x)g(x)\right)
=\frac{\partial f}{\partial x}g(x)
+f(x)\frac{\partial g}{\partial x} ∂ x ∂ ( f ( x ) g ( x ) ) = ∂ x ∂ f g ( x ) + f ( x ) ∂ x ∂ g Quy tắc cộng :
∂ ∂ x ( f ( x ) + g ( x ) ) = ∂ f ∂ x + ∂ g ∂ x \frac{\partial}{\partial x}(f(x) + g(x))
=\frac{\partial f}{\partial x}
+\frac{\partial g}{\partial x} ∂ x ∂ ( f ( x ) + g ( x )) = ∂ x ∂ f + ∂ x ∂ g Quy tắc dây chuyền :
∂ ∂ x f ( g ( x ) ) = ∂ f ∂ g ∂ g ∂ x \frac{\partial}{\partial x}f(g(x))
=\frac{\partial f}{\partial g}
\frac{\partial g}{\partial x} ∂ x ∂ f ( g ( x )) = ∂ g ∂ f ∂ x ∂ g 2.2.2. Gradient của vector-value function
Hay còn được gọi là Jacobian matrix của hàm R n ↦ R m R^n \mapsto R^m R n ↦ R m
J = ∇ x f = d f ( x ) d x = ( ∂ f ( x ) ∂ x 1 ⋯ ∂ f ( x ) ∂ x n ) = ( ∂ f 1 ( x ) ∂ x 1 ⋯ ∂ f 1 ( x ) ∂ x n ⋮ ⋱ ⋮ ∂ f m ( x ) ∂ x 1 ⋯ ∂ f m ( x ) ∂ x n ) \mathbf{J} = \nabla_{\mathbf{x}} \mathbf{f}
= \frac{d\mathbf{f}(\mathbf{x})}{d\mathbf{x}}
= \begin{pmatrix} \frac{\partial f(\mathbf{x})}{\partial x_1} & \cdots & \frac{\partial f(\mathbf{x})}{\partial x_n} \end{pmatrix}
= \begin{pmatrix} \frac{\partial f_1(\mathbf{x})}{\partial x_1} & \cdots & \frac{\partial f_1(\mathbf{x})}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m(\mathbf{x})}{\partial x_1} & \cdots & \frac{\partial f_m(\mathbf{x})}{\partial x_n} \end{pmatrix} J = ∇ x f = d x d f ( x ) = ( ∂ x 1 ∂ f ( x ) ⋯ ∂ x n ∂ f ( x ) ) = ∂ x 1 ∂ f 1 ( x ) ⋮ ∂ x 1 ∂ f m ( x ) ⋯ ⋱ ⋯ ∂ x n ∂ f 1 ( x ) ⋮ ∂ x n ∂ f m ( x ) 2.2.2.1. Gradient của vector-value function respect to ma trận
Xem xét hàm:
f ( x ) = A x , f ∈ R m , A ∈ R m × n , x ∈ R n \mathbf{f}(\mathbf{x}) = \mathbf{A}\mathbf{x}, \quad \mathbf{f} \in \mathbb{R}^m, \quad \mathbf{A} \in \mathbb{R}^{m \times n}, \quad \mathbf{x} \in \mathbb{R}^n f ( x ) = Ax , f ∈ R m , A ∈ R m × n , x ∈ R n Ta có:
f i = ∑ j = 1 n A i j x j f_i = \sum_{j=1}^n A_{ij} x_j f i = j = 1 ∑ n A ij x j Tổng quát hóa đạo hàm phần:
∂ f i ∂ A k l = { x l if i = k , 0 otherwise \frac{\partial f_i}{\partial A_{kl}} =
\begin{cases}
x_l & \text{if } i = k, \\
0 & \text{otherwise}
\end{cases} ∂ A k l ∂ f i = { x l 0 if i = k , otherwise hay
∂ f i ∂ A = ( 0 T ⋮ 0 T x T 0 T ⋮ 0 T ) ∈ R 1 × ( m × n ) \frac{\partial f_i}{\partial \mathbf{A}} =
\begin{pmatrix}
\mathbf{0}^T \\
\vdots \\
\mathbf{0}^T \\
\mathbf{x}^T \\
\mathbf{0}^T \\
\vdots \\
\mathbf{0}^T
\end{pmatrix}
\in \mathbb{R}^{1 \times (m \times n)} ∂ A ∂ f i = 0 T ⋮ 0 T x T 0 T ⋮ 0 T ∈ R 1 × ( m × n ) 2.2.3. Higher Order Derivatives
Xét hàm f : R n ↦ R , x ∈ R n f:R^n \mapsto R,\quad x \in R^n f : R n ↦ R , x ∈ R n
Nếu f f f ∂ ∂ x i ( ∂ f ∂ x j ) = ∂ ∂ x j ( ∂ f ∂ x i ) \frac{\partial}{\partial{x_{i}}}\left( \frac{\partial{f}}{\partial{x_j}} \right) = \frac{\partial}{\partial{x_{j}}}\left( \frac{\partial{f}}{\partial{x_i}} \right) ∂ x i ∂ ( ∂ x j ∂ f ) = ∂ x j ∂ ( ∂ x i ∂ f )
H x f = ( ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ) H_x f =
\begin{pmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{pmatrix} H x f = ∂ x 1 2 ∂ 2 f ⋮ ∂ x n ∂ x 1 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ⋮ ∂ x n ∂ x 2 ∂ 2 f ⋯ ⋱ ⋯ ∂ x 1 ∂ x n ∂ 2 f ⋮ ∂ x n 2 ∂ 2 f Khi f : R n ↦ R m , ∇ f ∈ R m × n f: R^n \mapsto R^m, \quad \nabla f \in R^{m\times n} f : R n ↦ R m , ∇ f ∈ R m × n
H x f ∈ R m × n × n H_{x}f \in R^{m\times n\times n} H x f ∈ R m × n × n